Don't be afraid of AC-coupled inputs

The module used to measure the effect of AC-coupling is an Intellijel Mixup.

Similar results can be obtained with any AC-coupled inputs.

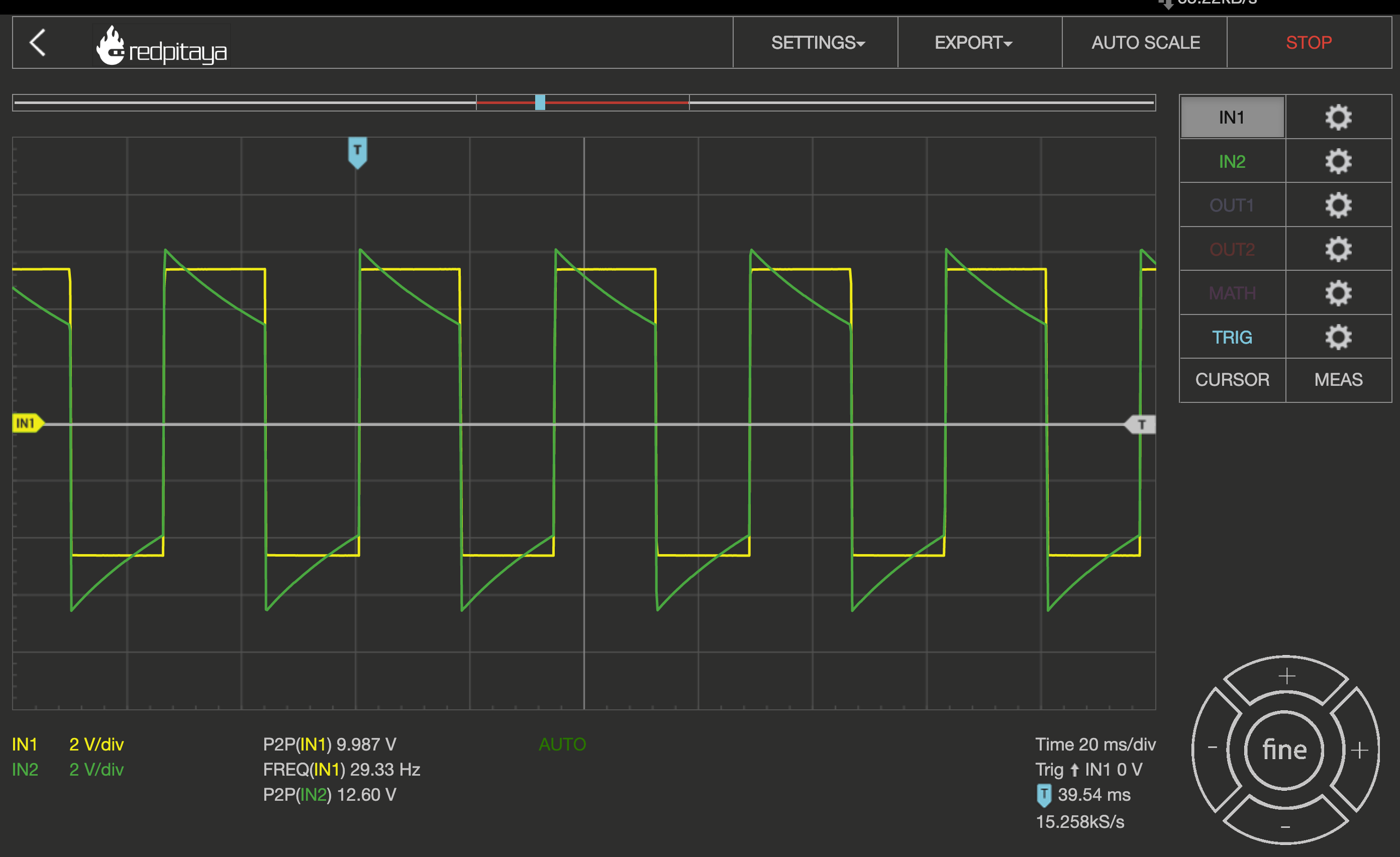
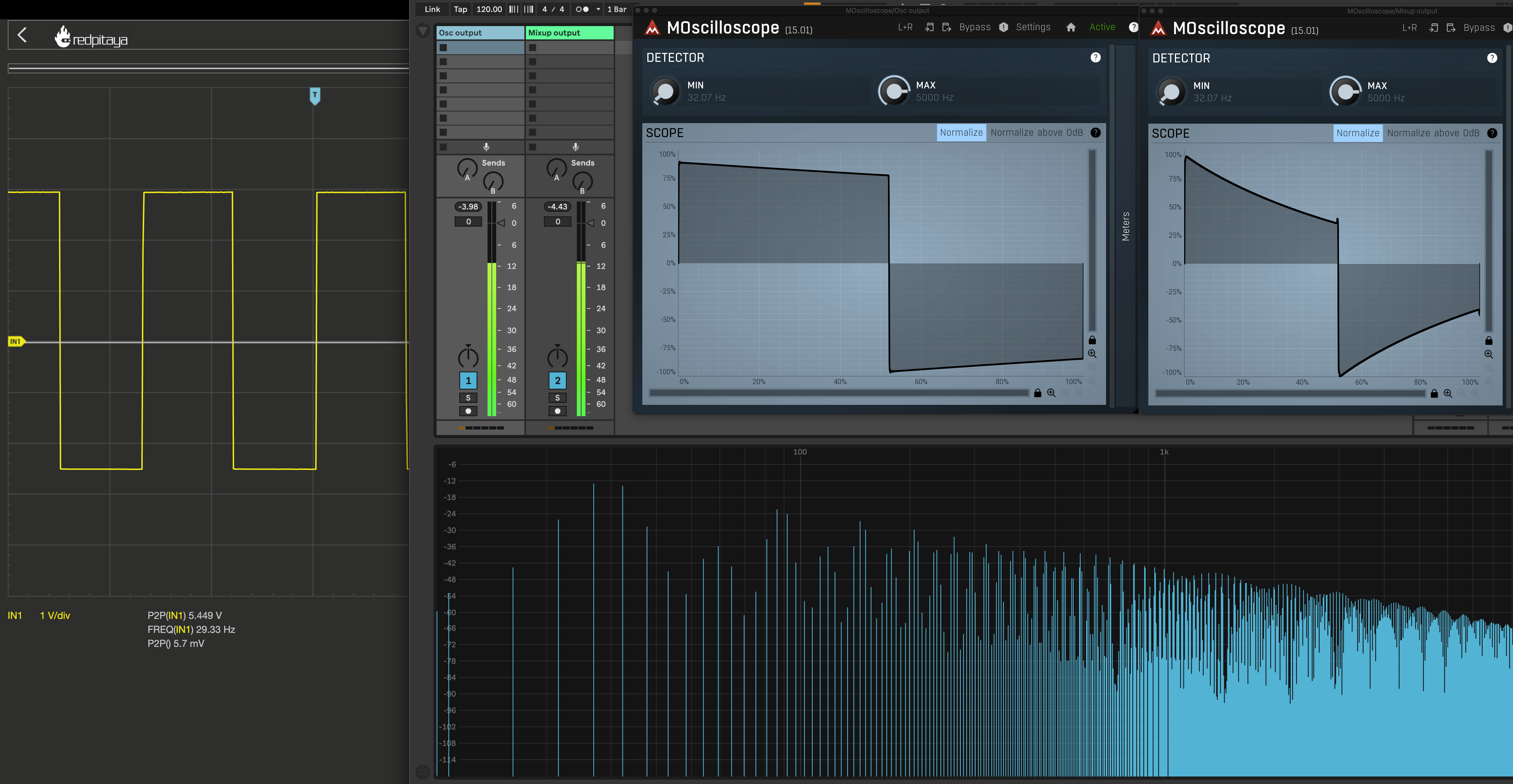
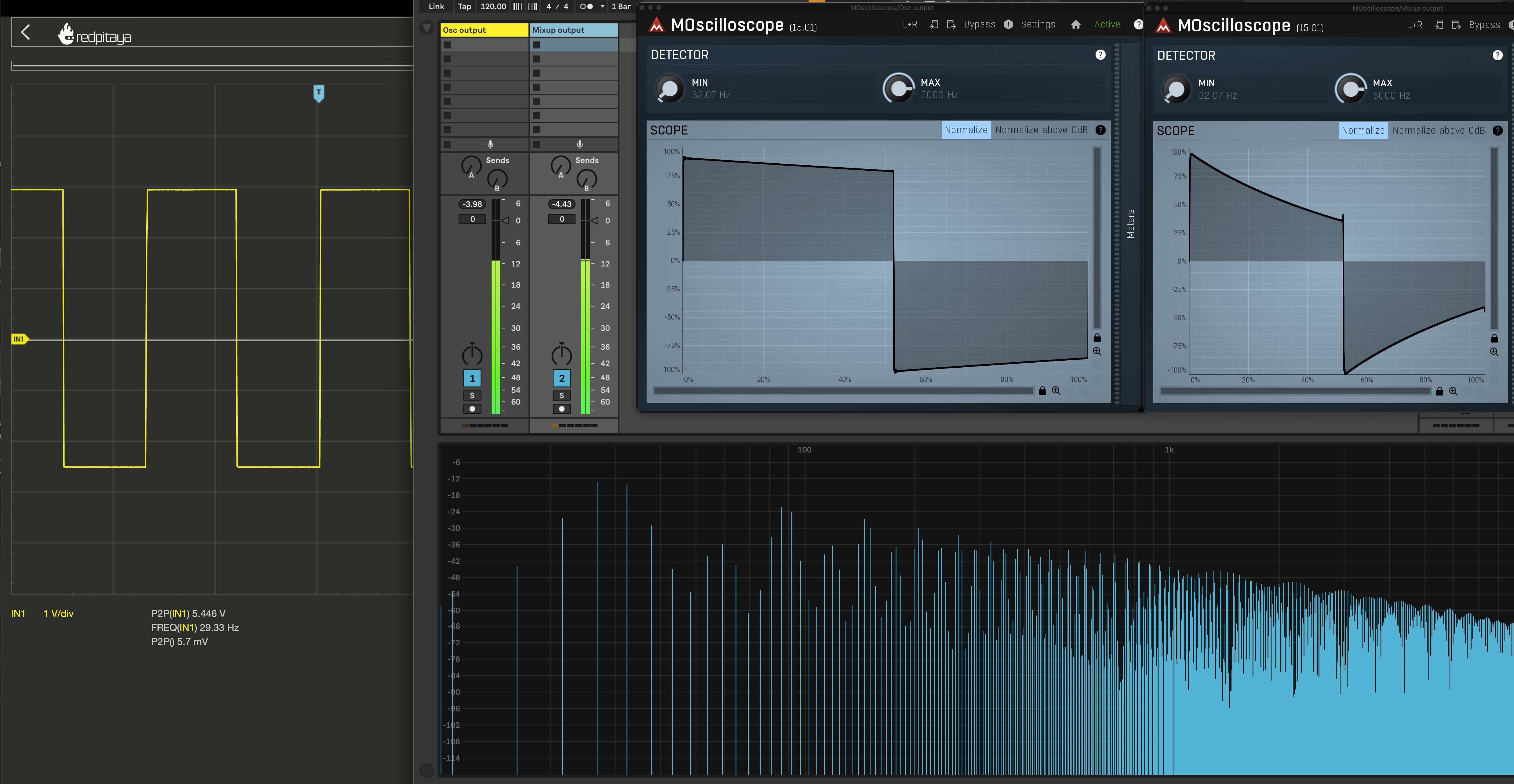
30Hz square wave :

The signal is generated with a Klavis Twin Waves MKII oscillator.

Before and after AC-coupling :

Spectrum before AC-coupling (oscillator output) :

Spectrum after AC-coupling (Mixup output) :

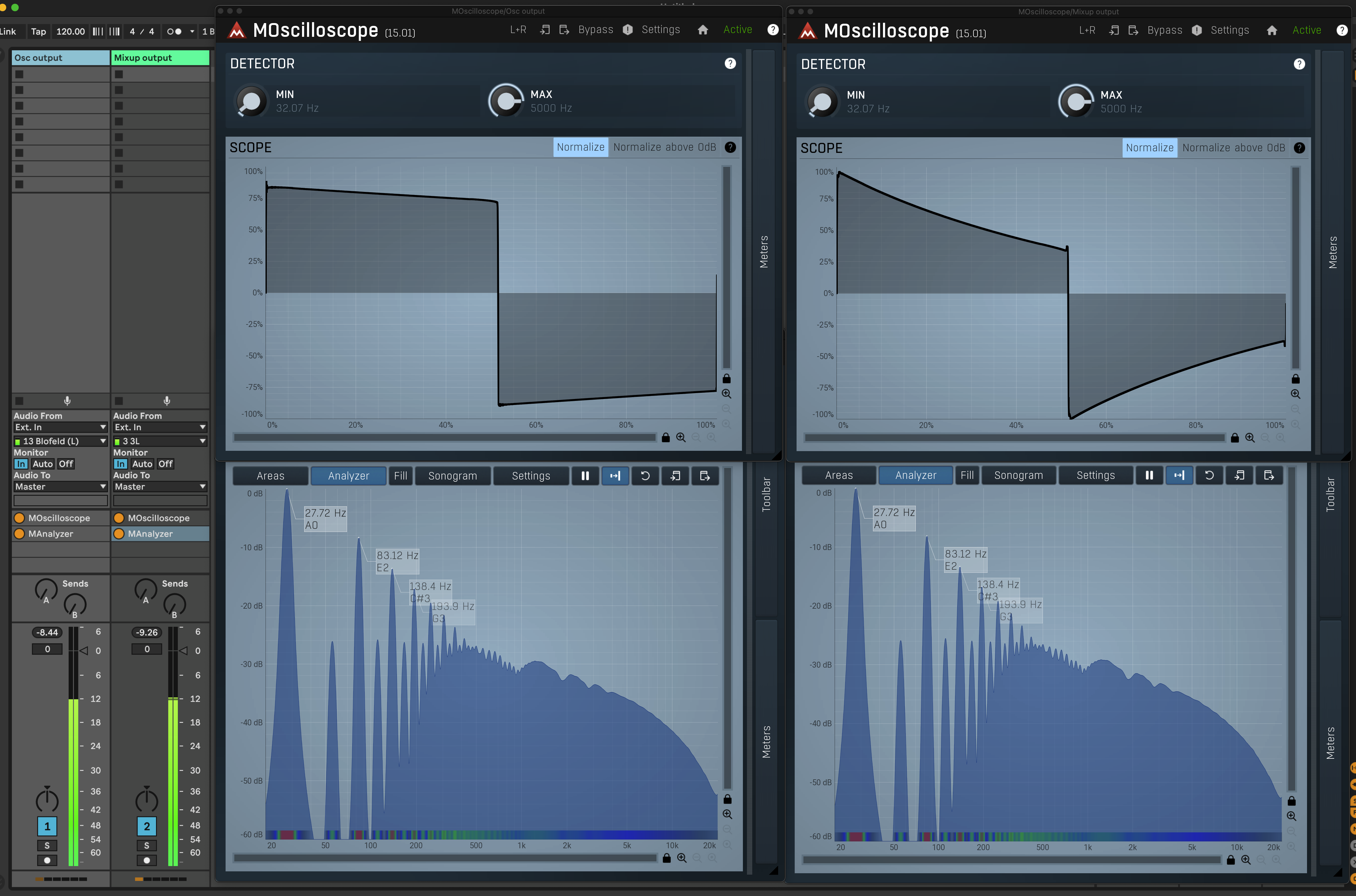
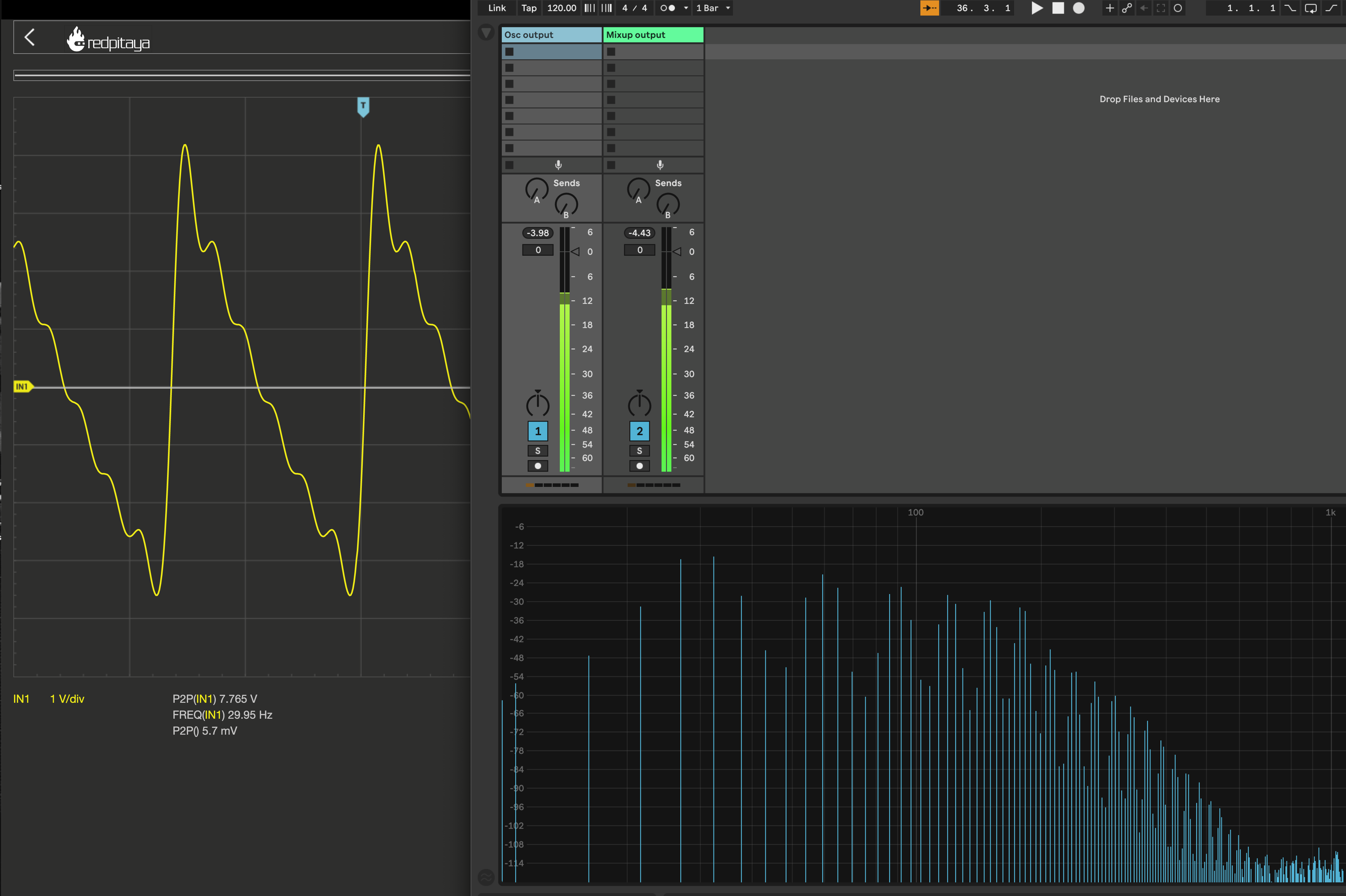
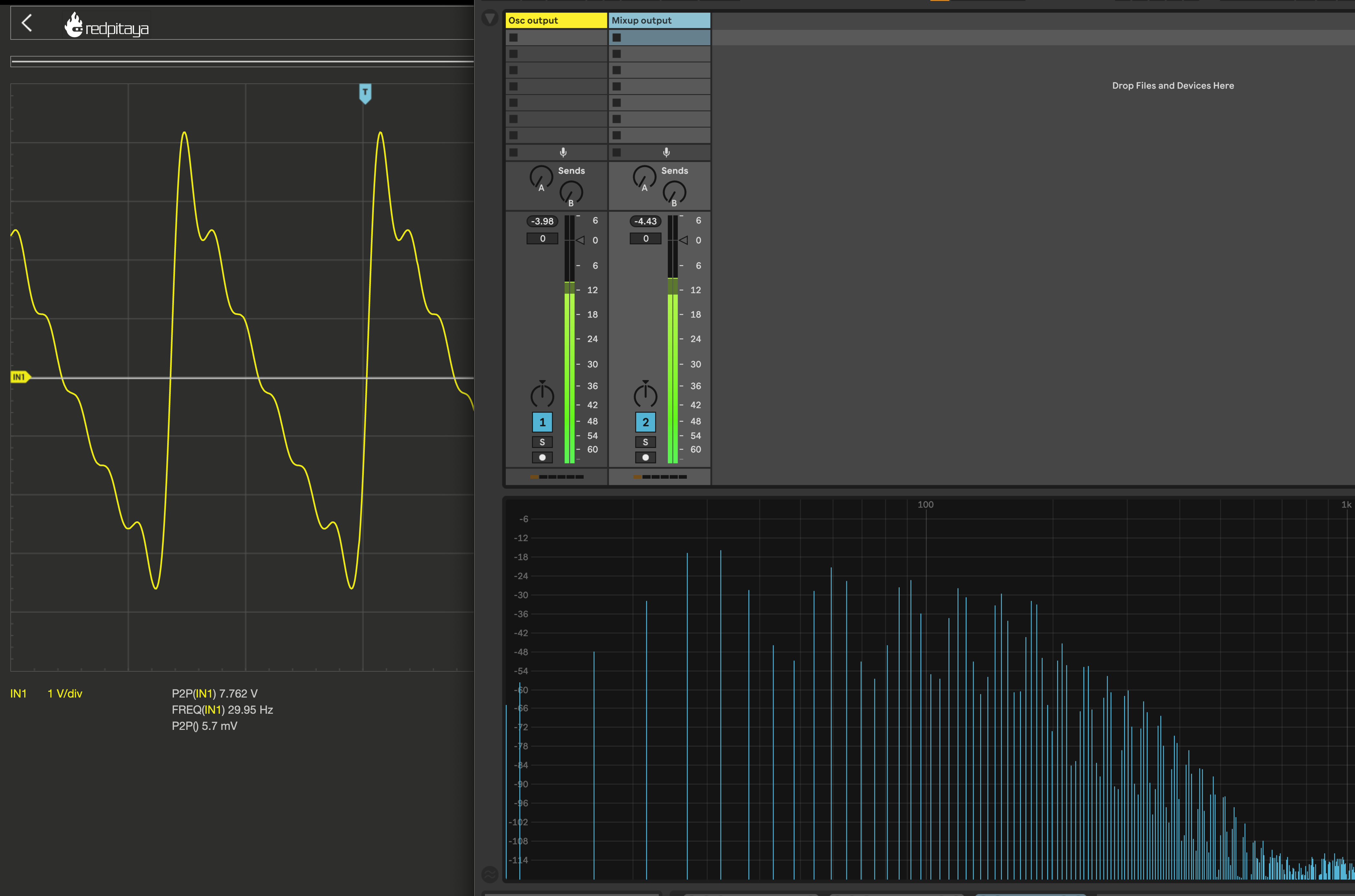
30Hz saw-like wave :

The signal is generated with a Xaoc Odessa oscillator.

Spectrum before AC-coupling (oscillator output) :

Spectrum after AC-coupling (Mixup output) :

Audio captures :

30 Hz square (50%) wave :

• Oscillator output
• Mixup output

30 Hz saw wave :

• Oscillator output
• Mixup output

30 Hz folded sin wave :

• Oscillator output
• Mixup output

Resources :

A very good explanation about AC coupling can be found in this Quora answer.